Compressing Neural Networks To See If They Learn

I’ve been thinking about the paper Understanding Deep Learning Requires Rethinking Generalization.

It asks: do neural networks trained with stochastic gradient descent learn anything?

It shows that neural networks have a lot of capacity. They can fit random labels and random data.

But they take longer to do so than with real data. You can see this by defining a 2 hidden-layer MLP that works on MNIST images. Initialize a network \(f\) and a copy \(\tilde{f}\). Train them on real data \(x, y\) and fake data \(x, \tilde{y}\).

So as far as I can tell, neural networks will use connections if ones exist, but will happily make them up if they don’t.

I decided to see if I could break neural networks trained on fake data.

Hypothesis

Assuming the “real-world data Manifold Hypothesis”, real data lies on a lower dimensional manifold of dimension \(d^{*} < d\), where \(d\) is the dimension of the space it’s embedded in. For example, a circle is a 1-dimensional manifold embedded in 2-dimensional space because you only need 1 coordinate (the angle) to describe your position on it.

So we should be able to compress our neural network (reduce the number of connections and/or units) without losing (much) accuracy. We only need enough units to fit functions of the data’s true dimensionality, assumed to be lower than the space’s.

Randomly generated data should lie on a manifold of higher dimension, as it lacks the connections real-world data has.

If we compress our network, we should see training accuracy drop off for the fake data, as it loses sufficient capacity to fit the data.

A network trained on real data should experience much less drop-off.

Some Ways This Could Fail

1. It’s not true.
2. The real data doesn’t lie on a low-dimensional manifold.
3. The fake data doesn’t lie on a low-dimensional manifold.
4. We don’t compress enough.
5. We compress too much and accuracy degrades too rapidly in both to distinguish them.

Methodology

We initialize 2 simple feedforward networks using the same random set of weights to ensure they start out identical.

We’re using MNIST to test this, because it’s simple and the paper mentioned above used CIFAR, which is also pretty simple.

The networks take in a 784-dimensional vector, pass it through one hidden layer of size \(512 \times 512\), and then to a softmax layer of size 10.

One network is trained on the actual MNIST dataset. The other one is trained on MNIST images, but with random labels. Both are trained for 100 epochs with a batch size of 128.

Each network is then compressed.

The code can be found here.

Compression

One way to compress a network \(f\) is to initialize a smaller network \(f'\), and then fit it to \(f\). We can do this by randomly generating data points \(x\) and using \(f(x)\) as the label.¹

We create a dataset of the same size as MNIST, but out of random noise, and then train on that.

Each iteration, there are 20% fewer hidden units.

Results

Red is fake, green is real.

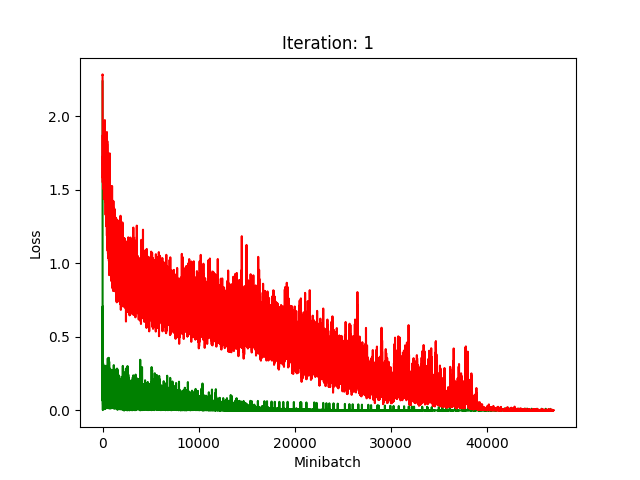
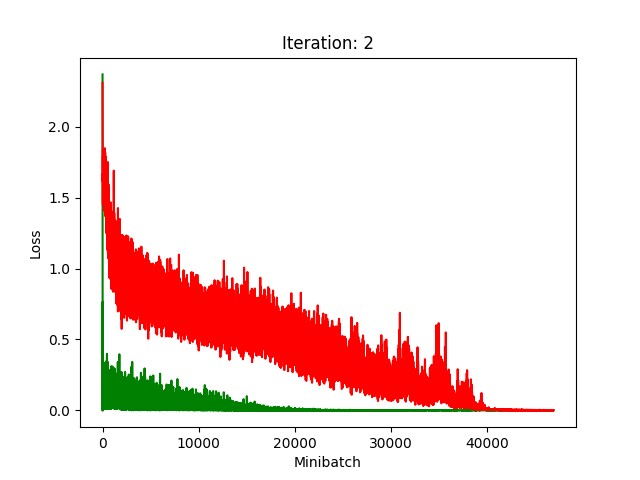
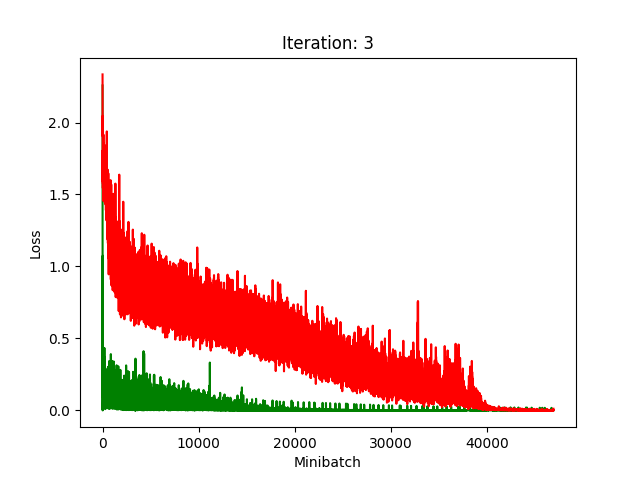
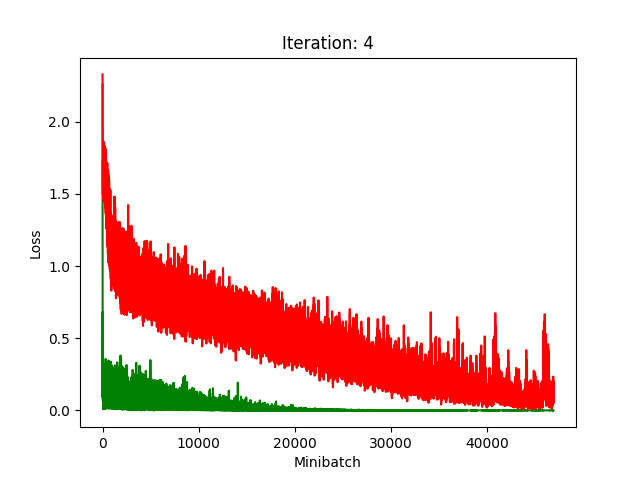
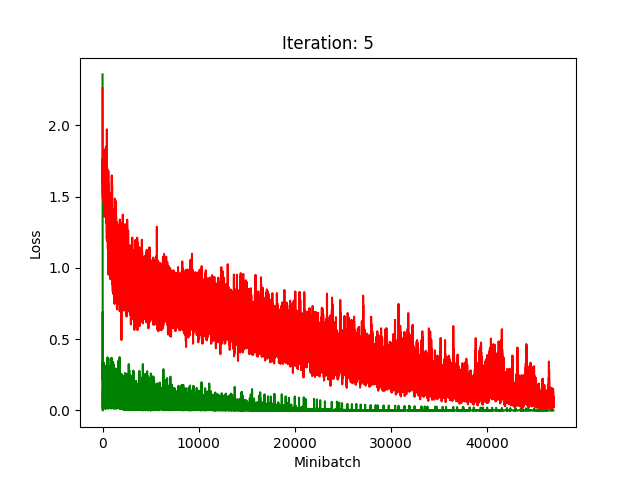
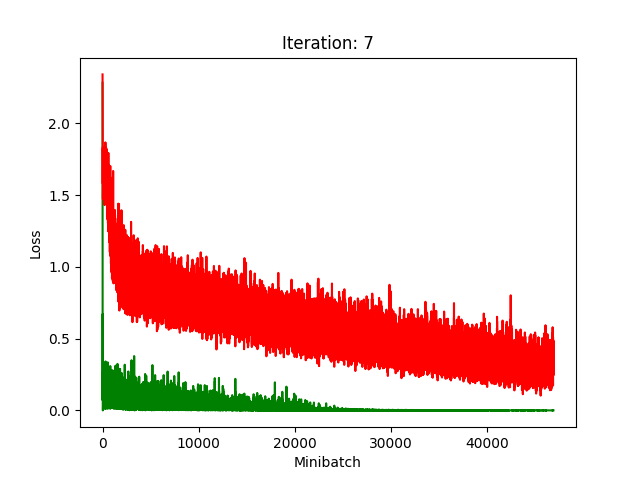
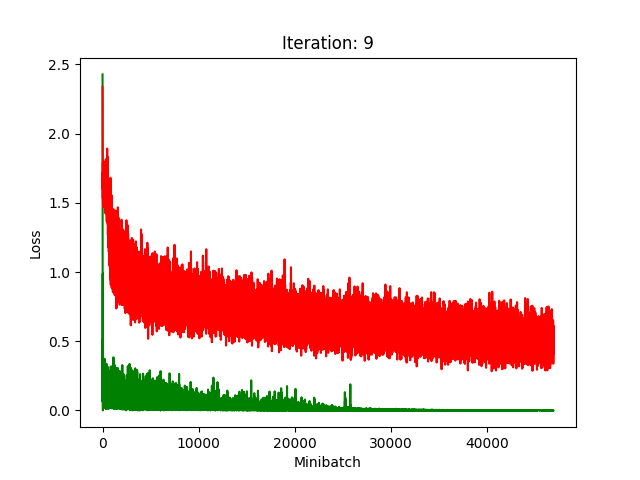
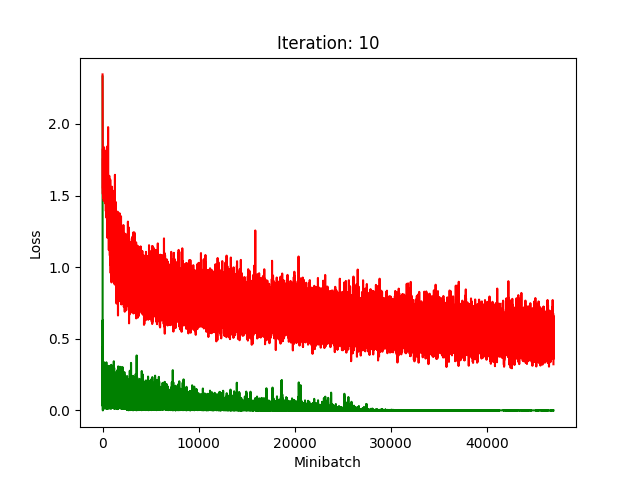
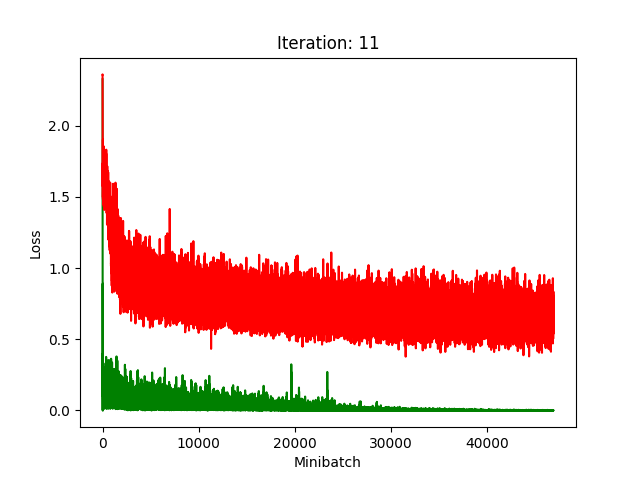
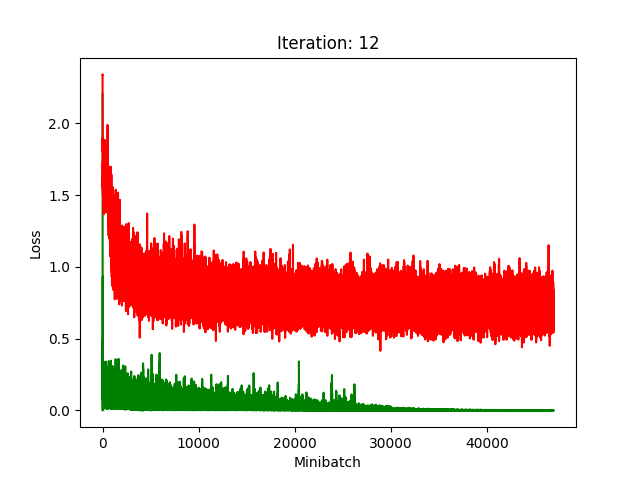
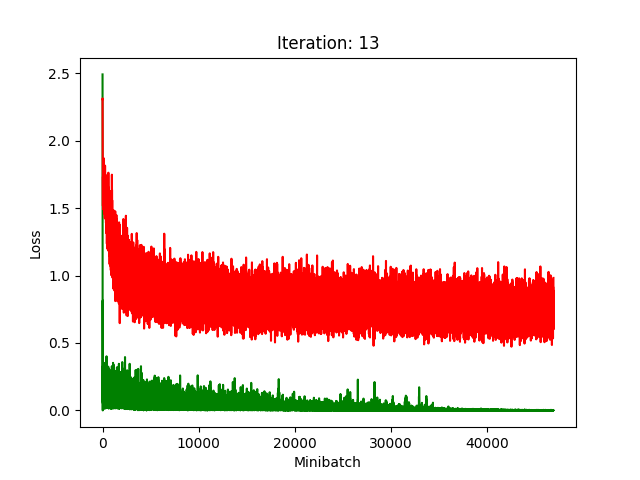
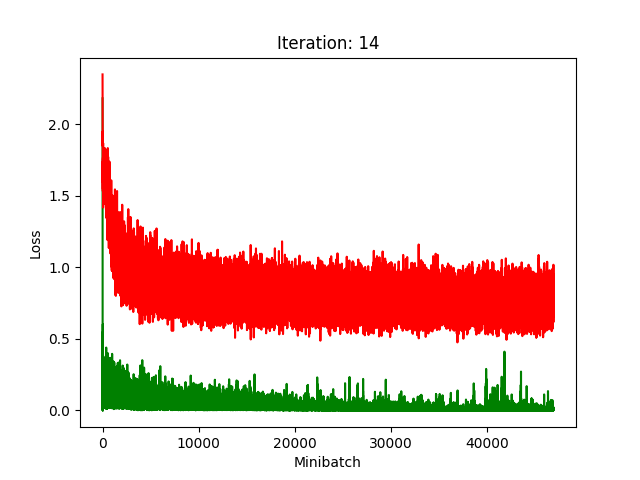
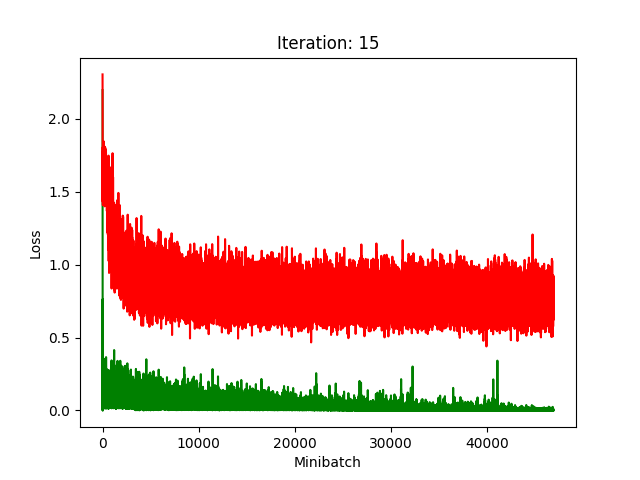
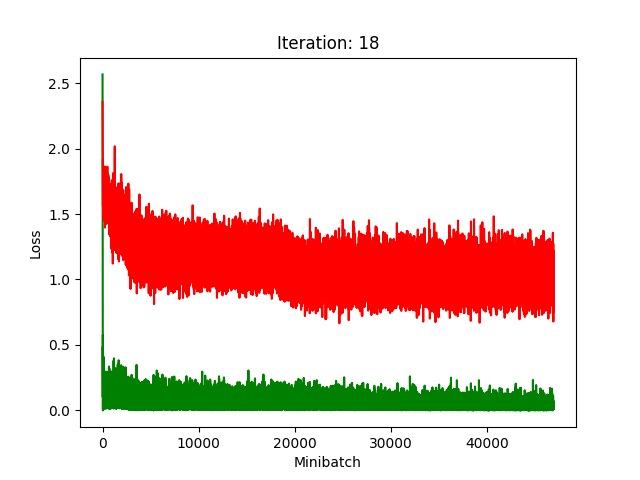
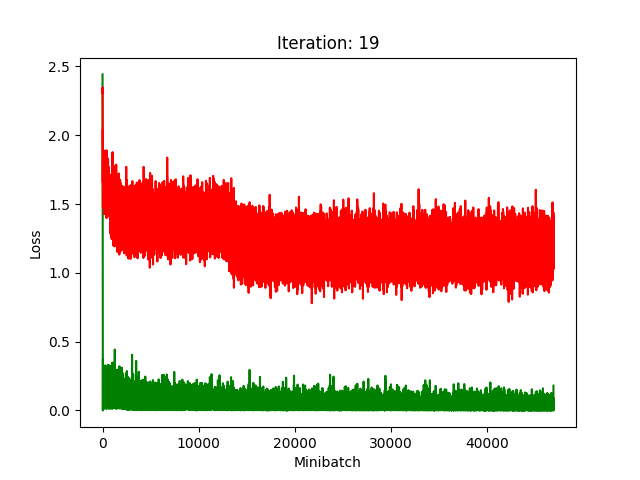
The real model trains faster, but the model trained on fake data still converges, at least for the first half.

Conclusion

Compression does indeed seem to hurt its performance more, as it clearly fails to converge after about 10 rounds of compression.

Future Directions

1. Test compressed models on original datasets.
2. Try different compression strategies.
3. Test on different dataset. CIFAR and ImageNet come to mind
4. Test on different size model. The differences may be more apparent in larger models.
5. Train for longer. This’ll need more GPUs.