But this is impossible by definition
The title may seem like a contradiction. How can you differentiate something that’s not even continuous?
The usual definition of the derivative of a function \(f\) at a point \(a\) is given by the limit:
\[f'(a) := \lim_{h \to 0} \frac{f(a + h) - f(a)}{h}\]If \(f\) is differentiable at \(a\), then it is continuous at \(a\). But what if it’s NOT even continuous? Then how the hell can it be differentiable?
Consider the step function, also known as the Heaviside step function. The Heaviside step function, \(H(x)\), is defined as:
\[H(x) = \begin{cases} 0 & \text{if } x < 0, \\ \frac{1}{2} & \text{if } x = 0, \\ 1 & \text{if } x > 0. \end{cases}\]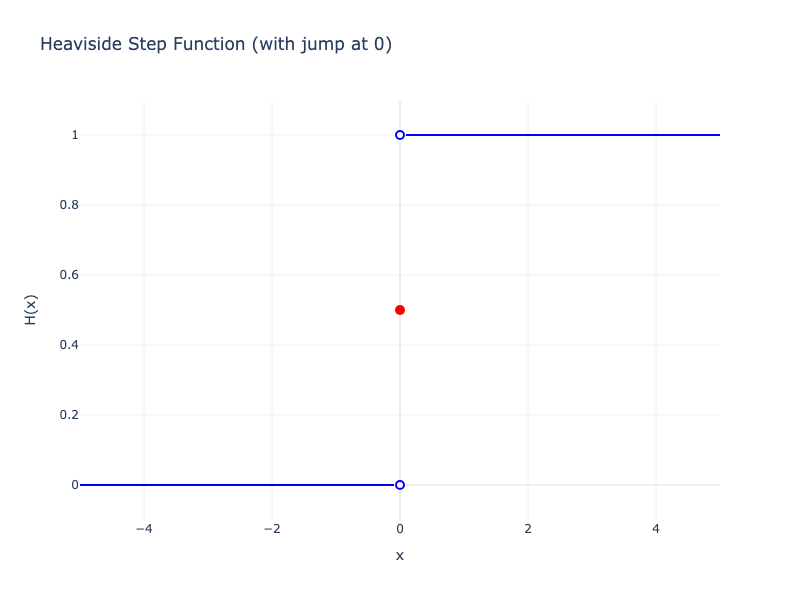
What’s its derivative? Forget the formal definition of the derivative for a moment, and just consider the step function and the intuitive idea of a derivative as a slope.
Outside of \(x = 0\), the step function is flat. So the derivative should be 0 everywhere besides \(x = 0\).
Look at the step function, left to right. At 0, supposing for a moment there is a derivative, then it can’t be any standard number. It’s not 0 since it’s certainly not flat. It’s not negative since it’s increasing to the right. It’s bigger than 1, 2, 3, 10000000000…
Since it goes from 0 to 1 in the space of a single point, the derivative would have to be infinitely big because its difference quotient is \(\frac{1 - 0}{0 - 0} = \frac{1}{0} = \infty\). The Problem is that no real number is infinitely big.
The usual way mathematicians deal with the Problem is to introduce generalized functions. They are also called distributions, which is confusing since probability distributions are completely different.
The formal definition of a generalized function is: an element of the continuous dual space of a space of smooth functions.
Well, what the fuck does that mean?
Luckily, you don’t have to care. The Problem was that no real number is infinitely big, so let’s just deal with that directly. Instead of introducing some abstract dual space of smooth functions, we can just enlarge the space of numbers. You’re used to this since childhood, ever since you first learned about negative numbers, irrational numbers, and imaginary numbers. This is one more enlargement.
The reason for the Problem is that we are really thinking about a line but identifying it with the real numbers. Identifying a line with the real numbers is just that – an identification – and it’s not even the best one.
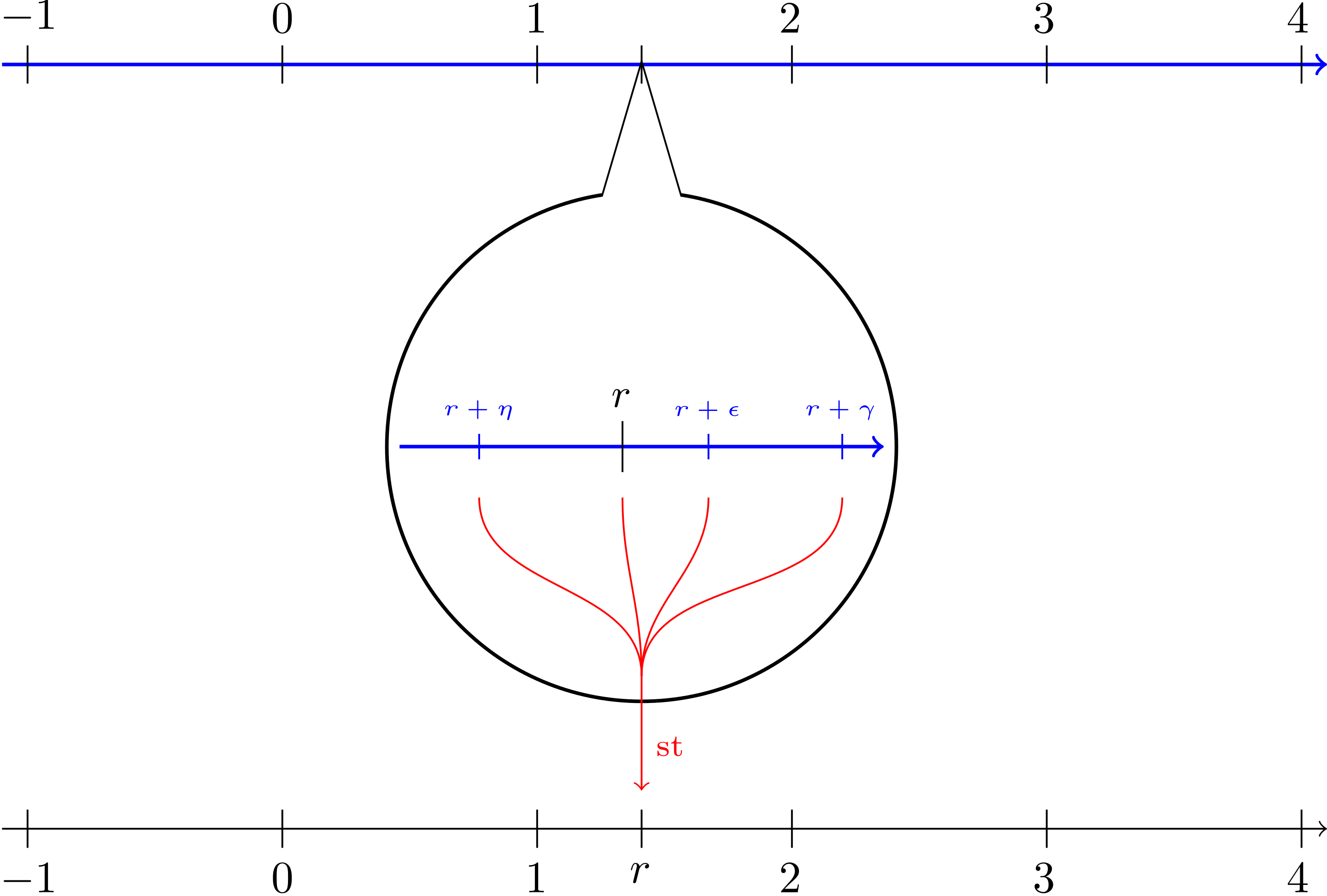
We’ll use the hyperreal numbers from the unsexily named field of nonstandard analysis to offer a radically elementary way of thinking about the problem. We will think of the line as the hyperreals rather than the reals. Consider this picture, where \(\omega\) is some infinite number, and \(\varepsilon\) is some infinitesimal number.
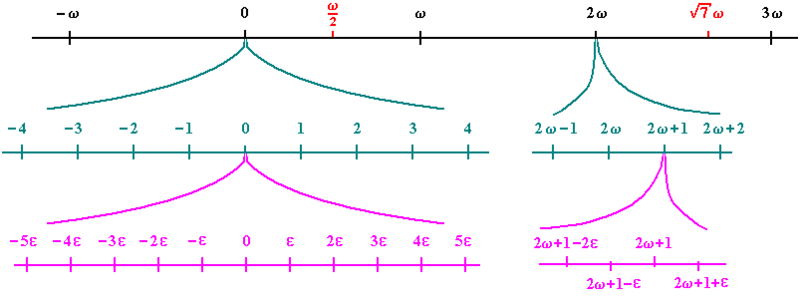
Now rather than a dual space, you may think of a fundamentally nonstandard function. Its domain or range (or both) are nonstandard. And unlike a generalized “function”, it’s a bona fide function, just not over the reals1. For the rest of this post, I will call the usual generalized functions “generalized functions” and this concept “nonstandard functions”. This class of nonstandard functions includes the generalized functions, but is bigger. Rather than cutting down the space of functions to a smaller space, we’re enlarging the space of numbers and functions between them.
Take the Dirac delta function. It’s infinitely tall, infinitely skinny, and has area 1 under it. So its nonzero domain is infinitesimal, and its range is infinitely big. We can formalize “infinitely tall, infinitely skinny, and has area 1 under it” very literally, as you’ll see. We will also free it from living only under an integral sign, like Cauchy did when he first defined it in 1827.2
What does it mean to be infinitely big?
A number \(N\) is infinitely big if \(N > 0,\ N > 1,\ N > 2,\ N > 9.3,\ N > 10000000\dots\) In other words, \(N\) is bigger than any standard number. This does not imply it’s the biggest number. There are (uncountably) many infinite numbers bigger than \(N\), and uncountably many infinite numbers smaller than \(N\). There are also countably many finite natural numbers smaller than \(N\). If \(N\) is a whole number, it’s called a hypernatural number, or sometimes hyperfinite.
Here are the hyperintegers \(\mathbb{Z}^{*}\), which are only the whole numbers, finite and infinite. As in, 0 fractional part.
A world in every grain of sand
A number \(\varepsilon\) is infinitesimal if it can be written as \(\frac{1}{N}\) for some infinitely big \(N\) (not necessarily a whole number \(N\)), or if it’s 0.
0 is the only number which is both standard and infinitesimal, and it’s the smallest infinitesimal. There is no second smallest infinitesimal, just like how there’s no second smallest positive real number.
We say 2 numbers \(a\) and \(b\) are infinitely close (in notation: \(a \approx b\)) if \(\vert a - b \vert\) is infinitesimal. This is an equivalence relation on the hyperreals, which divides them into infinitesimal neighborhoods. Because it’s an equivalence relation, the infinitesimal neighborhoods of different standard numbers are disjoint.
There is a standard part function, which takes a hyperreal number and gives you the standard real number that it’s infinitely close to. Infinitely big numbers have no standard part, since they’re not infinitely close to any real number. The standard part of an infinitesimal is 0.
What’s wrong with \(\infty\)?
The problem with \(\infty\) is that it’s not a number. It’s a concept used to describe the idea of something that’s unbounded or limitless. You can’t do full-on algebra with it.
Unlike the usual conception of infinity, \(N + 2.3\) is exactly 2.3 bigger than \(N\), whereas \(\infty + 2.3 = \infty\). This throws away valuable information. \(N-N/3\) is smaller by exactly \(N/3\). And so on. You can form expressions that previously were gibberish like \(N^{\frac{\pi}{N}} - N^{2.241} + 3 + \frac{1}{\sqrt{\frac{1}{N}}}\), but are now as meaningful as \(2+2\). Not as easy to compute though.
Examples of hyperfinite quantities
Here’s a video of an example since my friend Ben asked. It features some leaves since I was taking a walk.
The Number of Pieces an Integral is Cut Into
You’re probably familiar with the idea that each piece has infinitesimal width, but what about the question of ‘how MANY pieces are there?’. The answer to that is a hypernatural number. Let’s call it \(N\) again.
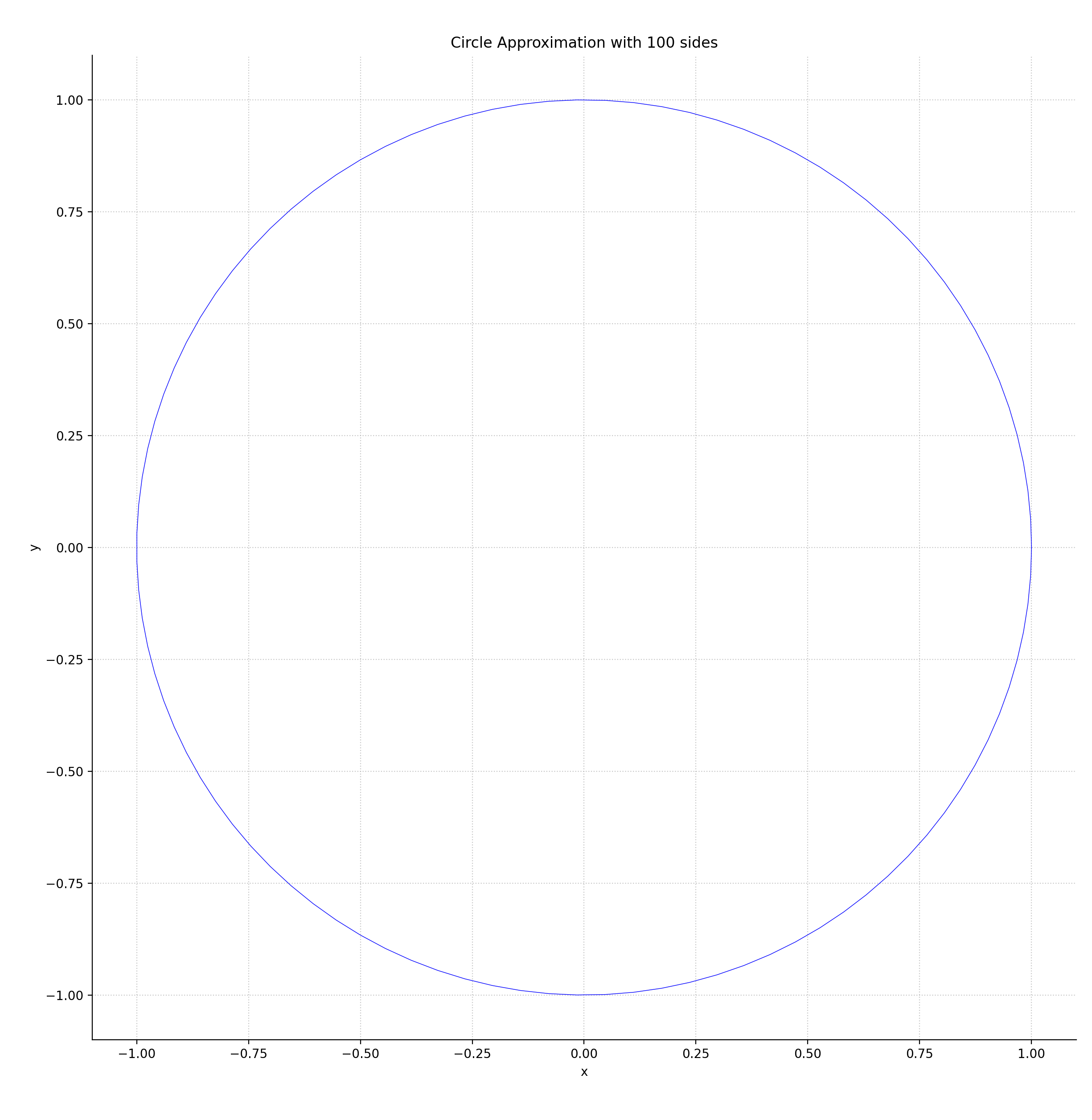
The Number of Sides of a Circle
Consider a circle as a regular polygon with infinitely many sides.
In the plot below, even 100 sides is barely discernible from a true circle.
The Number of Colors in the Spectrum
In our everyday experience, we perceive colors as a continuous spectrum, seamlessly transitioning from one hue to another. However, when we apply nonstandard analysis, we can think of the color spectrum as being divided into \(N\) distinct colors, where \(N\) is a hypernatural number.
Imagine splitting the visible spectrum, say from 400 nm (violet) to 700 nm (red), into \(N\) equally spaced colors. Each color occupies an infinitesimal range of wavelengths, or \(\Delta \lambda = \dfrac{300}{N}\ \text{nm}\). This captures one of the great uses of infinitesimals: 2 things that can be considered different or the same as needed. This captures the idea of shades of a single color. Imagine 2 shades of red—one a bit darker than the other. We can idealize this by saying they have infinitely close wavelengths, say \(700\ \text{nm}\) and \((700 - \varepsilon)\ \text{nm}\). In reality, shades are an non-infinitesimal wavelength apart, but because they can be arbitrarily close, this idealization is legit.
Germ of Generality: The Step Function
Now we’ll elaborate our running example: the step function \(H(x)\). We will “approximate” it by a nonstandard function. Keep in mind that this “approximation” is an approximation in the same way that a Riemann sum is an approximation to an integral. It’s infinitely close at every point.
We can model the step function dynamically or statically.
Dynamically: \(\lim_{N \to \infty} \frac{1}{1 + e^{-N \cdot x}}\). A sequence of logistic functions that approach the step function.
But we can do it statically as well. Instead of making a sequence, why not just use ONE number? We can skip to the end of the process and just let \(N\) be infinitely big.3
KEY POINT: Our nonstandard logistic function, the point of this whole post, is:
\[L(x) = \frac{1}{1 + e^{-N x}}\]This nonstandard logistic function is appreciably indiscernible from the step function. The difference between them is “one (standard) point thick”.
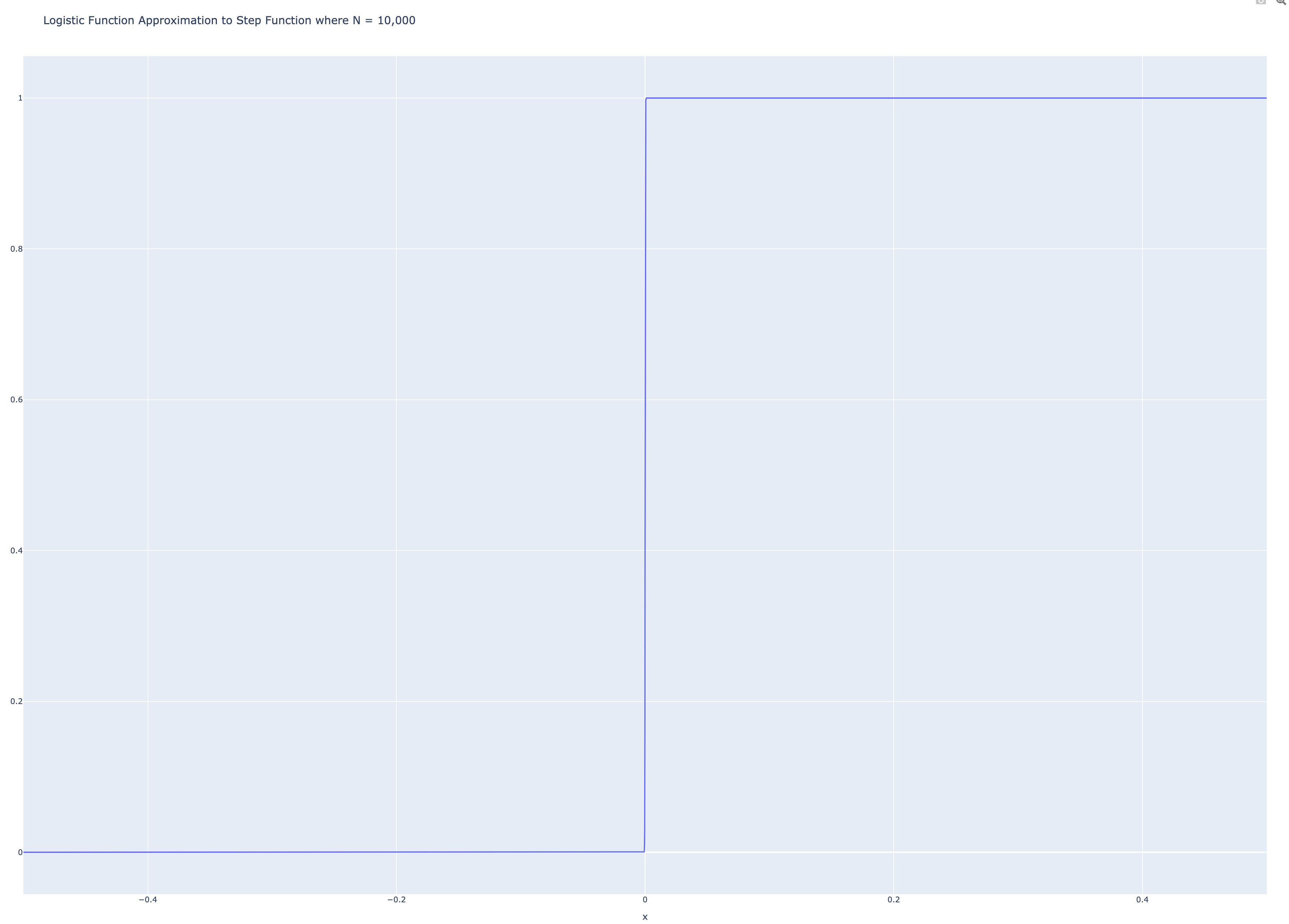
The Derivative of the Nonstandard Logistic Function
\(N\) may be infinite, but it’s still a FIXED number, AKA a constant.
KEY(ER) POINT: To take the derivative, you just, uh, take the derivative. Treat \(N\) as a constant and differentiate with respect to \(x\).
If you want a formal definition of this “new” derivative:
The derivative of a function \(f\) at a point \(a\) is:
\[f'(a) := \frac{f(a + \varepsilon) - f(a)}{\varepsilon}\]where \(\varepsilon\) is a fixed, nonzero infinitesimal. This definition captures the essence of the derivative without relying on limits. It’s worth noting that for standard differentiable functions, this definition agrees with the classical one (up to an infinitesimal difference that can be rounded away). So this is actually easier in a way, since you do the same thing with 1 less step (no limit).
If you did this with the usual definition of generalized functions, you wouldn’t figure out how to compute anything with them until about halfway through math grad school. Or never, since I just asked my friend Elliot Glazer and he said they never got to the actual computation, just the definition. But a motivated AP calculus high school student can do this. Helluva simplification.
DERIVATIVE:
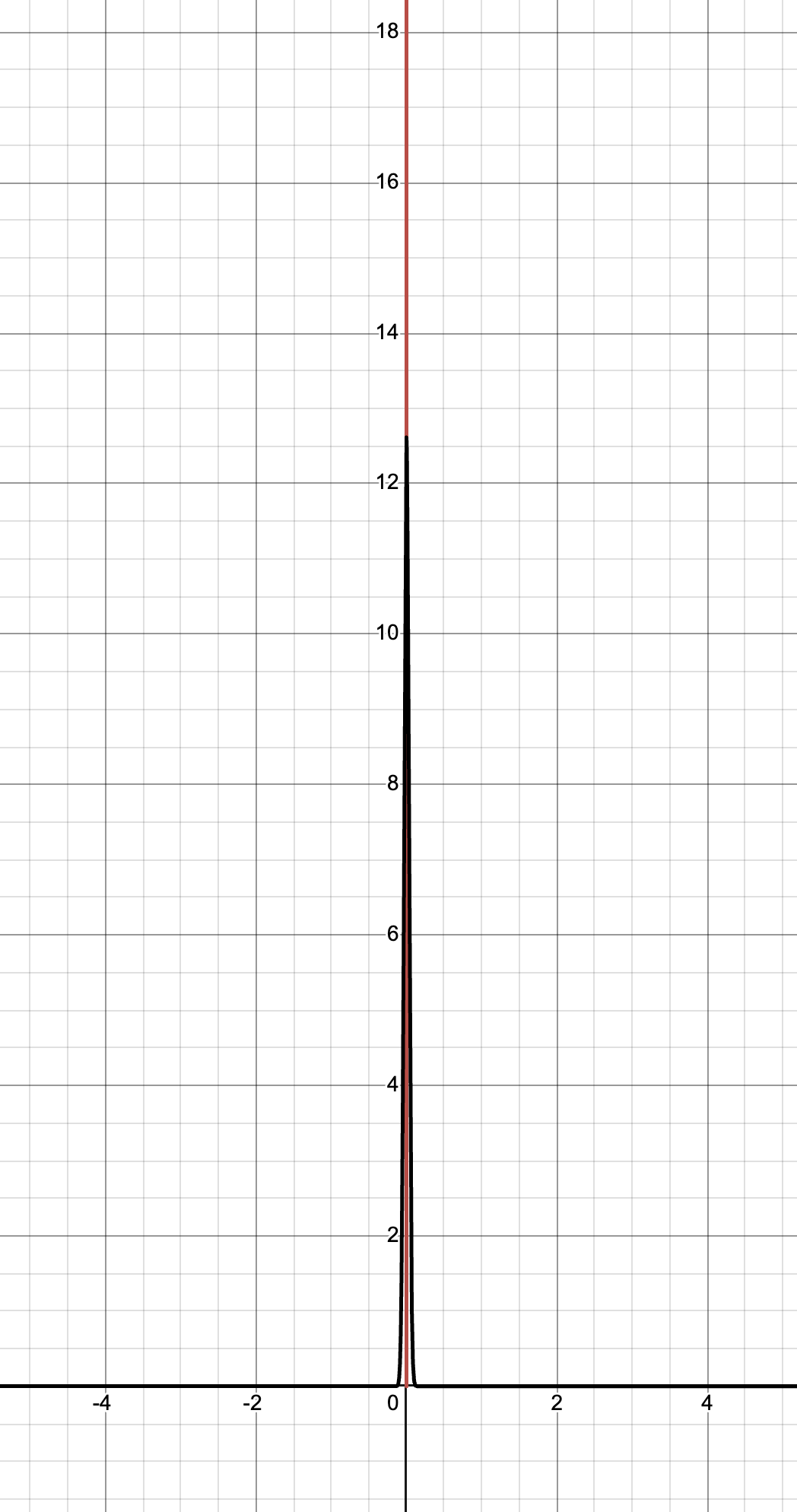
\[\frac{d}{dx} L(x) = \frac{d}{dx} \frac{1}{1 + e^{-Nx}} = \frac{N e^{-Nx}}{(e^{-Nx} + 1)^2}\]Here’s a graph of the derivative:
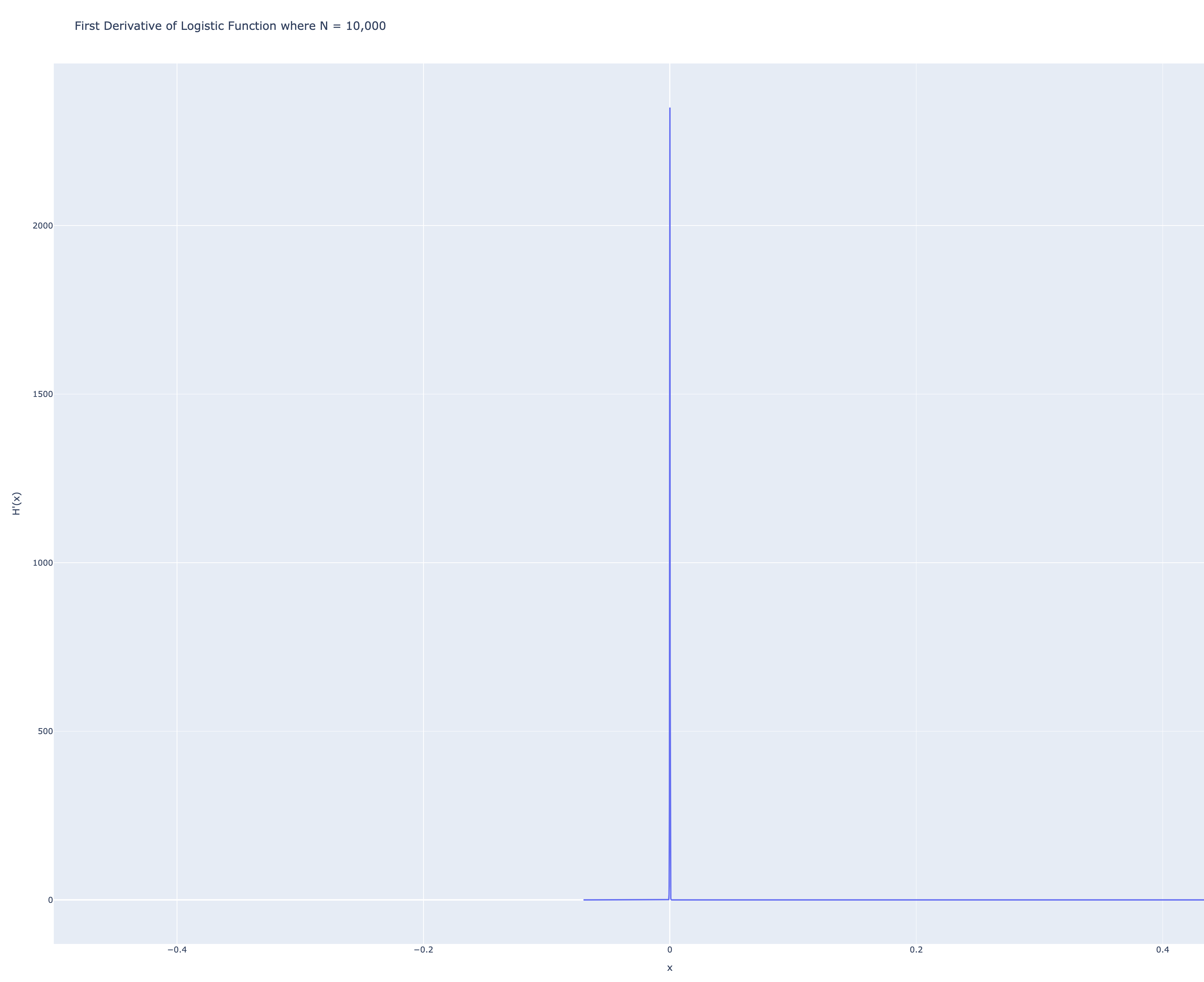
Spoiler alert: it’s the Dirac delta. Which makes sense, since the delta is (nearly) 0 everywhere except at the origin, where it’s infinitely big. Which is what we expected from the intuitive analysis.
Case Analysis: Exploring Different Regimes
Let’s analyze how the derivative behaves across different values of \(x\):
Positive appreciable \(x\) (Not infinitesimal and not 0)
A number is appreciable if it’s not infinitesimal. Y’know, big enough that you could appreciate (see) it.
Let’s plug in a (standard) positive rational number for \(x\) and see what we get.4 Since it’s rational, \(x = \frac{a}{b}\) for some standard coprime integers \(a\) and \(b\). Neither \(a\) nor \(b\) are 0.
Consider the subexpression \(N \frac{a}{b}\). If \(N\) is infinitely big, then \(Na\) is infinitely big too. If it wasn’t, then \(N\) wouldn’t be infinitely big. Same for \(\frac{N}{b}\). So \(N \frac{a}{b}\) is infinitely big. Let’s call it \(M\). \(N\) and \(M\) are of the same order because \(\frac{M}{N}\) is a standard number. Something that’s NOT of the same order is \(N\) and \(N^2\) because \(\frac{N^2}{N} = N\) which is not standard. If \(N\) is of order 1, then \(N^2\) is of order 2.
So we can replace \(e^{-N\frac{a}{b}}\) with \(e^{-M}\).
Now our expression is:
\[\frac{N e^{-M}}{(e^{-M} + 1)^2}\]Intuitively, \(e^{-M}\) is like \(e^{-\infty}\), which is 0. So \(e^{-M}\) should be infinitesimal. Using the Taylor series of \(e^{-M}\), we can see it’s an infinitesimal of (much) smaller order than \(N\). To make this a bit easier, first rewrite \(e^{-M}\) as \(e^{-M} = \frac{1}{e^{M}}\).
Let’s examine the Taylor series of \(\frac{1}{e^{M}}\) around \(x = 0\):
\[\frac{1}{e^{M}} = \frac{1}{1 + M + \frac{M^2}{2!} + \frac{M^3}{3!} + \frac{M^4}{4!} + \dots}\]Since \(M\) is infinitely large and positive, the denominator (\(e^M\)) is infinitely large. The series has a larger sum than any standard polynomial in \(M\) (or \(N\), since \(N\) and \(M\) have the same order), because it contains the term \(\frac{M^k}{k!}\) for every standard natural number \(k\). Because the later terms have higher order than previous, they are strictly larger regardless of the division by \(k!\) since \(k!\) is only finite but \(M^k\) is infinite and of a strictly larger order than all the previous terms.
This shows that \(\frac{1}{e^{M}}\) is infinitesimal since it’s 1 over something that’s infinitely big.
Then the numerator \(N e^{-M}\) is infinitesimal since it’s an order 1 infinite number times something that’s infinitesimal of (much) lower order.
The bottom term \(e^{-M} + 1\) is infinitely close to 1 by similar reasoning, so the whole denominator \((e^{-M} + 1)^2\) is also infinitely close to 1.
Putting it all together, the whole fraction is an infinitesimal number divided a number that’s nearly 1. AKA it’s infinitesimal. So outside of 0 it looks flat.
\[\frac{d}{dx} \frac{N e^{-Nx}}{(e^{-Nx} + 1)^2} = \frac{N e^{-N \frac{a}{b}}}{(e^{-N \frac{a}{b}} + 1)^2} = \frac{Ne^{-M}}{(e^{-M} + 1)^2} \approx \frac{e^{-M}}{1} = e^{-M} \approx 0\]Ditto for negative appreciable \(x\).
Infinitesimal nonzero \(x\)
This is a bit more complicated, since it depends on the order of \(x\). The short of it is that the logistic function is continuous, so by the Intermediate Value Theorem, it will take on all values from infinitesimal to infinite in the infinitesimal neighborhood of 0. All this “weirdness” is crammed into an infinitesimal slice of space, invisible if you took the standard part.
Let’s just take 1 specific value to illustrate. Consider \(x = \frac{1}{N}\).
The original formula is:
\[\frac{d}{dx} \frac{1}{1 + e^{-Nx}} = \frac{N e^{-Nx}}{(e^{-Nx} + 1)^2}\]Plugging in \(x = \frac{1}{N}\), we get:
\[\frac{N e^{-1}}{(e^{-1} + 1)^2} \approx .196 \cdot N\]So this particular value \(x = \frac{1}{N}\) has infinite derivative.
At \(x = 0\)
Remember that I said that 0 is the smallest infinitesimal? That means that any number (even an infinite one) times 0 is still 0. EXACTLY 0.
Exactly at \(x = 0\), the derivative becomes:
\[\frac{N e^{-N \cdot 0}}{(e^{-N \cdot 0} + 1)^2} = \frac{N e^0}{(e^0 + 1)^2} = \frac{N \cdot 1}{(1 + 1)^2} = \frac{N}{2^2} = \frac{N}{4}\]Since \(N\) is an infinite number, \(\frac{N}{4}\) is also infinite. This captures the essence of the Dirac delta function’s “infinite spike.” But now while the delta may be infinite, it has an end, a specific height. Which is \(\frac{N}{4}\).
This highlights something that is very difficult to even think about in the standard approach: the EXACT height of something infinitely tall. Delta functions are familiar to physicists and engineers, and they’re even familiar with the idea that the domain is infinitesimal. But the height is always treated as if it’s some sort of magic symbol called INFINITY. If you asked them ‘ok but HOW tall is it?’, they’d just say INFINITY. But here it’s not just infinite, but a specific infinite number divided by 4.
Let me tell you, people look at you funny if you say something is infinity over 4 tall. In the standard approach, \(\frac{\infty}{4}\) is just \(\infty\). But a physicist would NEVER mix up \(dx\) and \(dx^2\) because that would be confusing a line element with an area. So why not treat infinity the same way?
Higher derivatives
No reason to stop at the first derivative. The logistic function is infinitely differentiable, so we can just keep taking derivatives.
The second derivative is:
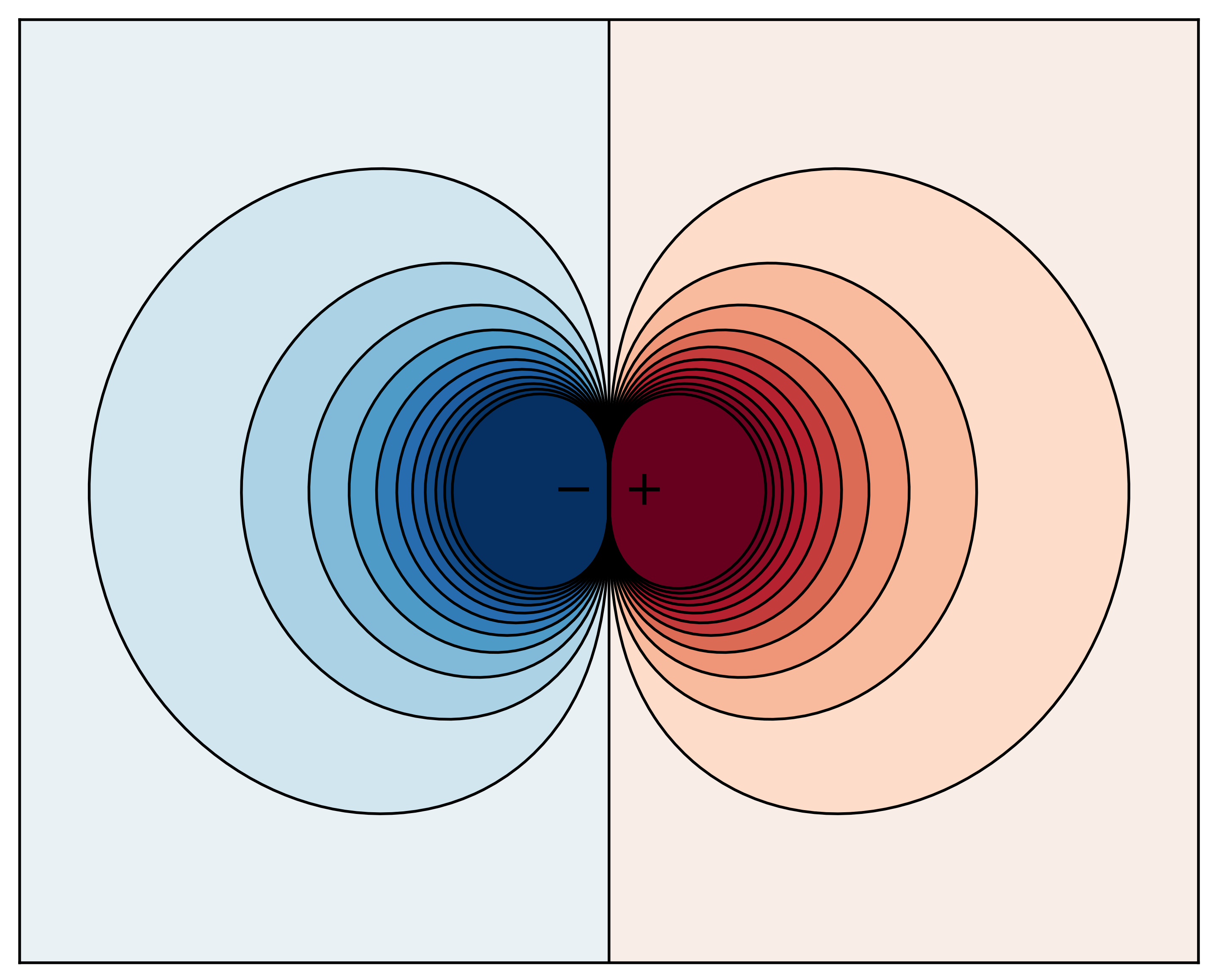
\[\frac{d^2}{dx^2}\left(\frac{N e^{-N x}}{(e^{-N x} + 1)^2}\right) = N \left(\frac{N^2 e^{-N x}}{(e^{-N x} + 1)^2} - \frac{4 N^2 e^{-2N x}}{(e^{-N x} + 1)^3} + e^{-N x} \left(\frac{6 N^2 e^{-2N x}}{(e^{-N x} + 1)^4} - \frac{2 N^2 e^{-N x}}{(e^{-N x} + 1)^3}\right)\right)\]This function is sometimes called the Laplacian of the indicator, or the dipole moment of a magnet.
Personally, I find the magnet picture intuitively helpful. A point charge flips from positive to negative in the space of a single point, and the closer you get, the higher the value of the magnetic potential. infinitely close to the magnet and the potential is infinitely big.
The graph of this one looks confusing plotted but here it is:
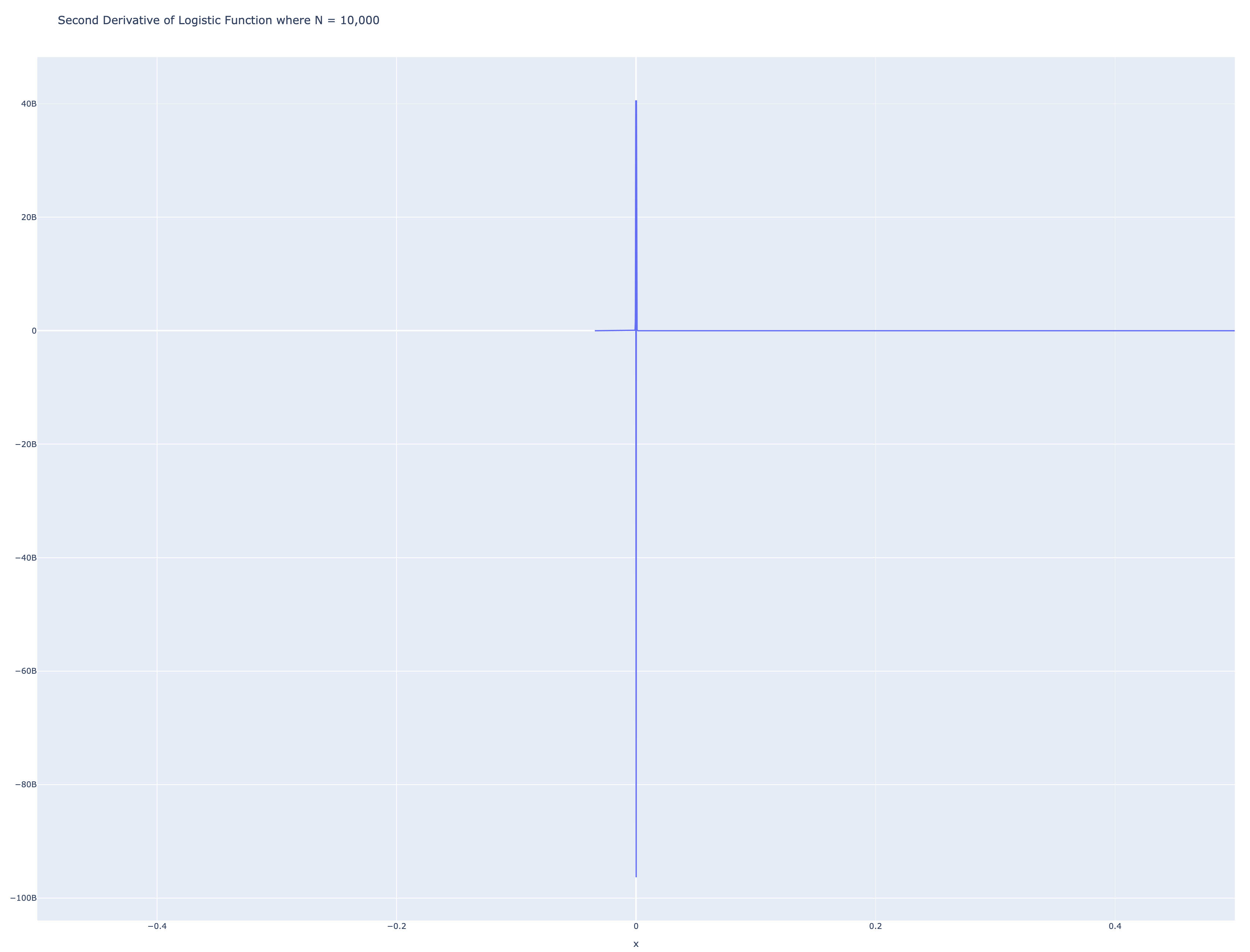
The higher derivatives are called multipole moments but I’ll stop at 2.
Conclusion
Sometimes, it’s easier to solve a problem by reexamining old assumptions than by introducing heavy machinery. Often.
By using nonstandard analysis and infinite numbers, we’ve found a way to differentiate the Heaviside step function using actual functions rather than distributions. This approach offers a more intuitive understanding of discontinuous functions and their derivatives, bridging the gap between mathematical rigor and intuitive comprehension.
In the realm of nonstandard analysis, infinite numbers aren’t obstacles but stepping stones—bridges that connect the discontinuities of mathematics with the continuity of intuition.
Here is a video I made on this. And a software library. And another software library. Here’s a calculator that works with infinitesimals and infinitely big numbers.
Credit to Euler, Cauchy, Mikhail Katz.
-
This concept can be extended far beyond the reals, but that’s a topic for another post. ↩
-
Differential forms are another thing nonstandard analysis can free from the tyranny of life under the yoke of the integral sign. But that’s for another post. ↩
-
How did I know to use the logistic function? Luck. Before that bums you out too much, keep in mind that determining whether a (standard or not) function is even continuous at a point is undecidable. That’s why no one gave you a general formula to find limits, because there isn’t one. This is just another example of that. ↩
-
The reason for rationals is that you can make them as close as you want to any real number, and they’re easy to work with. ↩